Chapter 4 The Neighborhood Stabilization Program and Voting
No man who owns his own house and lot can be a Communist. He has too much to do.
Complete data were available for 27,098 census tracts, covering more than half of the inhabited census tracts of 24 states, and more than half of the tracts where a self-described member of the Tea Party sought election. Most of the census tracts missing belonged to states where the process of connecting voting returns with census geography was infeasible. For instance, Michigan does not make clear the links between a voting tabulation district (VTD) as the Census Bureau defines it, and the county-precinct-ward system the state uses to publicize its results. For 15 other states, including Illinois, elections are so devolved that a state-wide election aggregation would have taken days to collect. Summary statistics for the complete data are available in the following table.
| Statistic | Mean | St. Dev. | Min | Median | Max |
| White % | 69.510 | 26.405 | 0.094 | 78.162 | 100.000 |
| Hispanic % | 14.917 | 19.349 | 0.000 | 6.930 | 98.499 |
| Black % | 8.581 | 13.724 | 0.000 | 3.416 | 98.361 |
| Asian % | 6.366 | 10.384 | 0.000 | 2.670 | 89.304 |
| 65-and-up % | 14.109 | 6.968 | 0.781 | 13.249 | 88.334 |
| Some college or less % | 67.824 | 18.317 | 0.000 | 71.584 | 100.000 |
| Median HHI (000s) | 62.663 | 26.421 | 12.934 | 56.250 | 250.001 |
| Density | 4,086.487 | 5,384.120 | 0.351 | 2,558.229 | 79,909.090 |
| Evangelical % | 14.261 | 10.260 | 0.000 | 11.224 | 103.566 |
| L.D.S. % | 1.355 | 1.460 | 0.000 | 0.910 | 22.616 |
| Population | 4,623.784 | 1,845.409 | 317 | 4,401 | 28,960 |
| Republican voting % | 50.283 | 20.136 | 0.000 | 50.626 | 100.000 |
| Miles to NSP1 | 5.287 | 2.868 | 0.001 | 5.111 | 10.866 |
| Mortgage occupancy % | 0.542 | 0.152 | 0.032 | 0.548 | 0.939 |
| Foreclosure rate | 2.617 | 1.621 | 0.000 | 2.263 | 13.792 |
| Labor variance | 6.092 | 3.917 | 0.230 | 4.808 | 33.994 |
| Unemployment change | 4.788 | 2.098 | 0.200 | 4.400 | 15.600 |
| Price change ’07–’10 | -9.370 | 9.160 | -52.382 | -6.889 | 15.789 |
| Tenure in home | 13.214 | 3.904 | 6 | 13 | 38 |
| Cook PVI | -1.690 | 6.870 | -19.305 | -1.541 | 13.146 |
While much of this analysis relies on data collected in 2010 census geographies, some key variables—including voting returns—were originally collected at a different geography. Translating these data to the census-tract level was fundamental to my analysis, so it is important that I describe the relationships between statistical geographies as well as my process of translation.
4.1 Relationships between statistical geographies
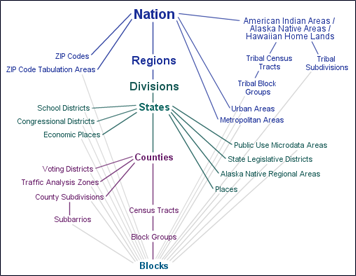 Figure 4.1: Organizational hierarchy of different geographies.
Figure 4.1: Organizational hierarchy of different geographies.
Census geography runs as follows. The basic unit, blocks, were originally designed for Census takers to walk, and so were constrained by physical boundaries difficult or illogical to cross. However, since the Bureau undertook to cover the entire United States with census blocks, there are millions of census blocks with no inhabitants, covering lakes, parks, and barren landscapes; this fact will become important shortly. Blocks are then aggregated into census tracts containing between 1,200 and 8,000 people. Tracts are the smallest unit for which American Community Survey data—a continuously-run telephone survey that collects additional demographic data such as median household income and educational attainment—are published. Census tracts sit inside counties and then inside states; unlike tracts and blocks, county boundaries are also legal jurisdictions and therefore rarely change. See Figure 4.1 for a graphical representation.160 Christopher Lemery, “United States Census Information @ Pitt: Understanding Census Geography,” LibGuides at University of Pittsburgh (https://pitt.libguides.com/uscensus/understandinggeography, March 2020).
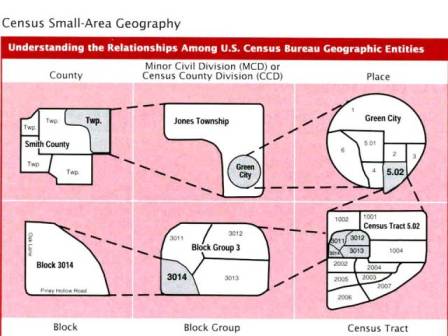 Figure 4.2: Relationships between different statistical entities
Figure 4.2: Relationships between different statistical entities
While tracts and blocks were designed to be semi-permanent, acting as the basis for other, non-Census areas, in practice their shapes shift with population changes. These shifts mean that: (a) not all 2000 tracts and 2010 tracts are congruent (though many are); and (b) non-Census areas (such as state-designed voting precincts) can cut census blocks. Figure 4.2 shows the Census Bureau’s graphical representation of geographical relationships. Since these Census Bureau does not make public the responses of individual persons or homes until several decades after, placing each record in its appropriate area is impossible. Rather, ecological methods approximate the distribution of persons, votes, or homes among geographies. Ecological methods assume that persons, votes, or homes are equally distributed throughout an area: ecological methods would assume, for instance, that since six percent of Americans are millionaires, then six out of every hundred persons sampled—no matter their neighborhood—would also be millionaires. Strictly speaking, ecological methods are logical fallacies of de-composition, of taking the whole for the part. However, guided by the right principles, ecological methods can be perfectly valid statistical tools.
The first principle is that smaller geographies are better. Take for example tract 12099005947, a nearly-optimal tract of 4,406 people in Palm Beach County. The owner occupation rate is 97%, and 88% of the residents are aged 65 or older. However, Palm Beach County entire contains tracts with as low as 4% 65-and-up, and owner occupancy rates around 33%. Taking the county for the tract would poorly represent the diversity within Palm Beach, smoothing out the nuances that differentiate one neighborhood’s politics from the next. Zooming in on census tracts improves the accuracy of ecological methods, allowing for a fuller picture.
The second principle is that errors should be distributed evenly. Errors here refer mainly to one party’s votes that are misplaced among another party’s voters, a result of the process by which voter tabulation districts must be decomposed and recomposed in order to translate non–2010 Census geography into 2010 Census geography. This assumption may not always hold in my data: the history of American urban planning has shown that physical barriers—the same used to bound census blocks—often bind communities in more ways than one. But since census tracts are also (if more weakly) constrained by physical boundaries, the aggregation of census blocks into tracts ought to be roughly consistent with the physical construction of communities by planners. Additionally, most voting precincts do not cut tracts. This means that the nightmare problem of gerrymandering deliberately undermining the assumption of evenly-distributed errors should be a moot point. Gerrymandering divides districts into a biased collection of precincts, it does not redraw precinct lines. Since my analysis deals with already-made and locally-created voting precincts, it skirts this particular problem potentially befalling analyses that begin at the county or Congressional-district level.
4.2 Data collection and aggregation
I built my data almost exclusively from official statistics and estimates. Given that most of my sources would eventually lead back to the Census Bureau, which covers the entire United States, I knew that the factors limiting my coverage would lie outside the Census Bureau. Collecting and translating precinct-level voting data to census tracts proved to be the most limited and time-consuming aspect of this process. I began by downloading precinct-level voting returns from the Harvard Election Data Archive (HEDA).161 Stephen Ansolabehere, Maxwell Palmer, and Amanda Lee, “Precinct-Level Election Data, 2002-2012” (Harvard Dataverse, 2014). Started in 2008 by political scientists, this database compiled voting returns from most states and reported results for state and national races in a standardized format.
These figures were then wedded to files specifying the geographic boundaries of each voting precinct within a state. This stage saw the complete loss of several states’ data as some systems used to identify precincts at the state-level were inconsistent with Census Bureau naming conventions. For each state, I looked for an isomorphic mapping from state-level naming to the standardized naming of the Census Bureau or Harvard Election Data Archive, and only for links where the match was clear were the data used. Case in point was Maryland: the voting returns data clearly contained every single specified tract in Maryland, but matching algorithms could only identify a few hundred of the several thousand voting districts. Geographic files came primarily from the Census Bureau’s TIGER/Line redistricting project, the official database for all Census geography,162 “2010 TIGER/Line Shapefiles” (US Census Bureau, 2012). via the Election-Geodata mapping project, an open-source repository for redistricting data,163 Nathaniel V. Kelso, “Nvkelso/Election-Geodata,” March 2020. though, as alluded to above, some states’ geographic files were also compiled by HEDA.
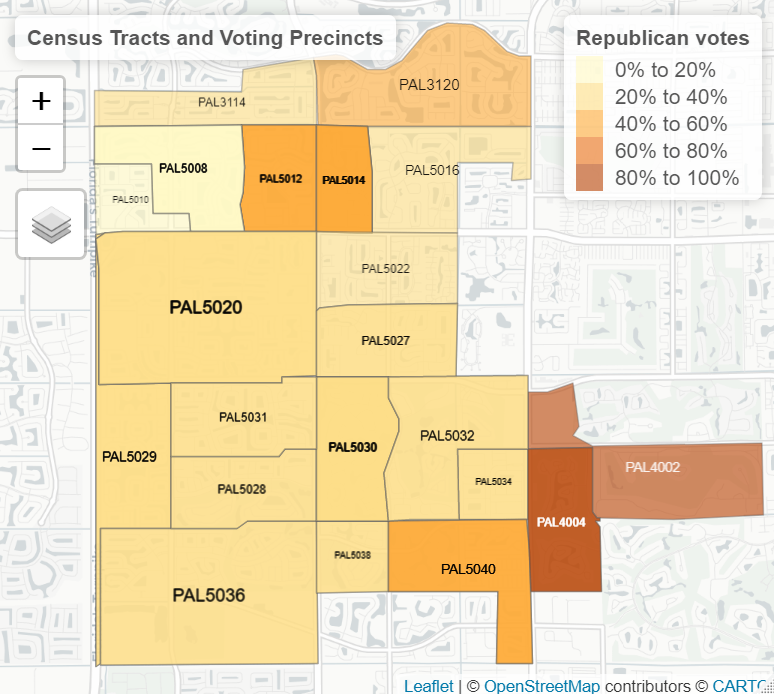 Figure 4.3: Voting precincts and census tracts in Palm Beach County, Florida without census tracts…
Figure 4.3: Voting precincts and census tracts in Palm Beach County, Florida without census tracts…
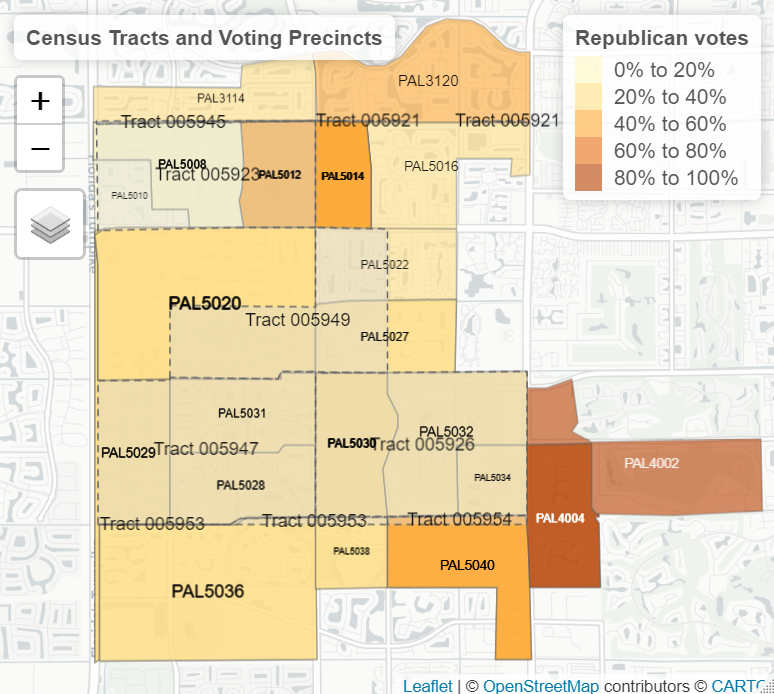 Figure 4.4: …and with census tracts.
Figure 4.4: …and with census tracts.
Translating the voting precincts to Census geography was a complicated process of decomposition and recomposition. Since tracts often straddle two voting precincts, distributing votes to particular tracts relies on ecological methods, essentially peeling off the part of a precinct lying in one tract and stitching it together with parts of the other precincts that also coincide with a tract. This process generates Frankenstein tracts, where 20% of one precinct’s votes are summed with 100% of a second precinct’s votes and 3% of a third precinct’s votes, depending on how much of a precinct coincides with a tract. Since the voting records of these tracts are purely statistical constructions, it is perfectly fine that one have fractions of votes. Take again, for example, our tract 12099005947 in Palm Beach County Florida: it recorded 732.00 Republican votes out of 3114.00 total votes in the 2010 Congressional race. But it’s neighbor, tract 12099005949, recorded 461.85 Republican votes against 1414.25 total votes.
There is, however, more than one way to cut a census tract. The obvious way to slice census tracts is by geography: the spatial intersection forms the basis for dividing up votes. The better way to slice census tracts is by voting-age population: the intersection of eligible people forms the basis for dividing up votes. This method better leverages even more granular data that the Census Bureau publishes to partially overcome ecological approximations and account for differing population densities within tracts. The way tracts in exurban and coastal areas are created necessitates this approach. Ideal census tracts are fairly homogeneous in terms of density, as it is the goal of the Census Bureau to preserve neighborhoods and actual street blocks where possible. In contrast, tracts containing blocks where population density begins to shift can be quite irregular. Since tract size is constrained by population, tracts not only can subsume those zero-population blocks I mentioned earlier, but must subsume some uninhabited blocks.
Public Law 94-171 (PL 94-171) ensures that the Congressional districting mandate of equally-populated districts be met with small-area population counts. In addition, requirements of the Voting Rights Act pressed states to consider the racial makeup of their Congressional districts. Since these are governmental tabulations, the population counts were required to be public. I drew from these data tables, comprising every block in the United States, in order to divide up census tracts. The advantage from data granularity is large: half of the 11,166,336 census blocks in 2010 were smaller than a tenth of a square mile164 “FCC Form 477: More About Census Blocks” (Federal Communications Commission, March 2015), 1.—Charlottesville itself contains 803 census blocks, averaging 54.14 persons.165 “2010 Census Summary File 1” (US Census Bureau, 2011).
\[\begin{equation} votes_{t} = \sum_{p=1}^{P \cap t} votes_p \cdot \frac{\sum_{b=1}^{B \cap t} VAP_b}{\sum_{b=1}^{B} VAP_b} \end{equation}\] Where t represents a particular tract, p a precinct from the set P of precincts intersecting with that particular tract, and b a block from the set B of blocks within that particular precinct:
Then, to distribute portions of voting precincts to tracts, I counted how many census blocks from each particular tract lay within each precinct. For computational reasons, the relevant statistic here was the block’s spatial center rather than its nuanced boundaries. Since blocks are so small, and voting precincts are supposed to be fashioned from census blocks (known exceptions exist in a handful of states), using the entire boundaries of a block would likely have generated errors that had more to do with the resolution of downloadable mapping files than actual, in-practice boundaries. Summing up the voting-age population (the census does not ask about citizenship status or felonious histories) of those blocks that lay within a particular precinct, and then comparing that figure to the total voting-age population of said precinct, allocates the percentage of votes from a precinct to a tract. This method is represented formally to the right. To recap, this process first decomposes precincts into blocks, and then recomposes precincts from tracts (where the block-tract connection is trivial by construction). Each tract is allocated votes according to its share of the total precinct population.
Each tract in this dataset was allocated votes by this method, with the exception of Californian tracts. The Redistricting Database for the State of California, hosted at the University of California Berkeley School of Law, had already performed a more precise version of this process using voting registration records.166 “2010 General Election Precinct Data” (University of California, 2011). Voter registration records allow researchers to locate each address—and thus each resident voter—precisely within tracts and precincts. A more careful version of my analysis would implement such methods, but the time required would have exceeded my timeframe.
A similar process of de/recomposition was used for the Department of Housing and Urban Development’s foreclosure data,167 Shawn J Bucholtz, “Neighborhood Level Foreclosure Data” (Department of Housing & Urban Development Office of Policy Development and Research, September 2008); Mirian Cody, “Neighborhood Stabilization Program Data,” Research Portal, HUD User (https://www.huduser.gov/portal/datasets/NSP.html, October 2010); Todd Richardson, “NSP2 Data and Methodology,” Research Portal, HUD User (https://www.huduser.gov/portal/NSP2datadesc.html, December 2009). which was tabulated at the 2000 tract- and block group–level. While most of these tracts are the same, and almost all 2010 tracts only subdivide a single 2000 tract, updates to geographic surveying, changes in the landforms, and population fluctuations necessitate updated tracts. The Census Bureau publishes relationship files that precisely place the percentage of housing units within each tract and block group in their 2010 equivalents. Housing units were used here instead of persons since the relevant statistics concern properties, not people. I first decomposed 2000 tracts by the percentage of housing units intersecting with a particular 2010 tract, and then recomposed those 2010 tract figures by allocating foreclosure starts and total housing units according to the percentage each 2010 tract contained.
Lastly, data from the 2010 US Religion Census168 Clifford Grammich et al., “U.S. Religion Census Religious Congregations and Membership Study, 2010 (County File)” (Open Science Framework, 2018). and the Bureau of Labor Statistics169 “Local Area Unemployment Statistics” (Bureau of Labor Statistics, March 2020). were collected at the county-level. Since tract geography follows county geography, I simply joined those county figures to each tract, so for each tract the county average was used. All other data used were native to the 2010 tract level, without translation. They came primarily from the 2010 decennial census,170 “SF1”; Kyle Walker and Bob Rudis, “Tigris: Load Census TIGER/Line Shapefiles,” February 2020. with some additional information from the 2005-2009 American Community Survey.171 “2006-2010 American Community Survey 5-Year Summary File” (US Census Bureau, 2011); Kyle Walker, Kris Eberwein, and Matt Herman, “Tidycensus: Load US Census Boundary and Attribute Data as ’Tidyverse’ and ’Sf’-Ready Data Frames,” January 2020. American Community Survey data comes attached with margins of error, but, as no other variables had these margins of error, they were entirely ignored so as not to complicate calculations. In the interest of time and data quantity, I took the Census Bureau at their word that errors were distributed evenly.
Outside the Census Bureau, the Federal Housing Finance Agency located addresses within their 2010 tracts, requiring no further pre-processing. Those data were constructed from tens of millions of federally-financed home loans. By virtue of that source, the indices are only composed of prime mortgages. However, two factors work in my favor here. First, significantly more prime mortgages than subprime mortgages defaulted during the foreclosure crisis.172 Ferreira and Gyourko, “A New Look at the U.S. Foreclosure Crisis.” Second, the FHFA’s index only considers properties with at least 100 sales (and purchases).173 Alexander Bogin, William Doerner, and William Larson, “Local House Price Dynamics: New Indices and Stylized Facts,” Real Estate Economics 47, no. 2 (June 2019): 365–98, https://doi.org/10.1111/1540-6229.12233. This feature matters because housing prices are strongly dependent spatially: nearby homes with nonconforming mortgages will likely sell for similar amounts as homes with conforming mortgages. Still, this limitation means that some tracts with high levels of nonconforming loans were omitted. There are many neighborhoods, for instance, with complete homogeneity of conforming or nonconforming loans, enclaves connected by mortgage brokers who handled large numbers of subprime loans or specific developments.174 Dayen, Chain of Title. The political behavior of these developments is interesting due to their uniformity, but beside the aims of this thesis.
4.3 Data Analysis
My approach is simple: I will test my assumption that the Neighborhood Stabilization Program increased housing prices; then, I will model the effect of the NSP on voting with and without home price controls. If the NSP did raise home prices, then its presence ought to be associated with an increase in Republican voting over the model that controls for home prices, where no change in voting should be associated with the NSP. Additionally, this section allows for the possibility that impacts on voting were sharpened where housing was politically stigmatized by Tea Party politics, as Chapter 2 suggested. To evaluate those localized effects, trials are run that only include tracts in which a Tea Party candidate ran for office.
4.3.1 Did NSP1 increase home prices?
The following table lists the effects of NSP1 on prices. Additional models remove state-level fixed effects and variables that were included in the allocation formula for NSP1, and thus covary highly with which tracts actually received NSP1 funding. To avoid price spillovers from interfering with measurement, I only included tracts which were at least 1 mile away from a tract receiving NSP1 funding. The results are plain and robust to several possible covariates: tracts receiving NSP1 funding were associated with statistically significant home prices declines, estimated between one and two points lower, compared to tracts not receiving aid.
| Dependent variable: | |||
| Home price index change, 2007-2010 | |||
| (1) | (2) | (3) | |
| NSP1 | -1.3690*** | -2.0434*** | -1.4835*** |
| Labor risk | 0.7081*** | -0.0917** | 1.0440*** |
| 2010 unemployment rate | 0.3360*** | 1.6545*** | -0.4795*** |
| Median household income | 0.0599*** | -0.0621*** | 0.0855*** |
| 2009 foreclosure rate | -1.0080*** | -1.1952*** | -1.0763*** |
| Mortgaged occupancy rate | -19.2162*** | -2.2096* | -24.8948*** |
| 2010 forelcosure rate | -0.3587 | -1.2888*** | 0.4197 |
| Population density | 0.0001*** | 0.0001*** | 0.0002*** |
| 65-and-up % | 0.0298*** | -0.0796*** | 0.0445** |
| Tenure in home | 0.6415*** | 0.9509*** | 0.9359*** |
| Squared tenure | -0.0122*** | -0.0169*** | -0.0217*** |
| White % | 0.3396*** | 0.8572*** | 0.2442*** |
| Black % | 0.3127*** | 0.8950*** | 0.2416*** |
| Hispanic % | 0.2026*** | 0.6302*** | 0.1269*** |
| Asian % | 0.3590*** | 0.7857*** | 0.2284*** |
| Unemployment change ’05–’10 | -1.0173*** | -3.6583*** | 0.8717*** |
| High-cost mortgage rate | 0.5058*** | 0.4215*** | |
| Seriously delinquent rate | -1.6806*** | -2.1938*** | |
| Constant | -50.0030*** | -86.0479*** | -42.5166*** |
| State fixed Effects? | Y | N | Y |
| Observations | 11,992 | 11,992 | 3,683 |
| R2 | 0.8520 | 0.7851 | 0.8587 |
| Adjusted R2 | 0.8516 | 0.7848 | 0.8575 |
| Residual Std. Error | 6.8560 | 8.2569 | 7.1414 |
| F Statistic | 2,151.3950*** | 2,429.8210*** | 715.8556*** |
| Note: | p<0.1; p<0.05; p<0.01 | ||
 Figure 4.5: Residuals on fitted values from price estimation
Figure 4.5: Residuals on fitted values from price estimation
 Figure 4.6: Sample quantiles on theoretical quantiles.
Figure 4.6: Sample quantiles on theoretical quantiles.
Results (not shown) of these models using NSP2 tracts, allocated competitively within the universe of at-risk tracts, are similarly sobering. The estimated negative impacts agree with results from a HUD evaluation of the Neighborhood Stabilization Program’s second round of funding, which found insignificant-to-negative changes in home prices.175 Jonathan Spader et al., “The Evaluation of the Neighborhood Stabilization Program” (U.S. Department of Housing and Urban Development, March 2015). Further, these models appear to be good predictors of home prices, accounting for 78% to 85% of total price variation among the 11,992 tracts included.
Differential effects of NSP1 in Tea Party tracts are explored in Model 3. These results closely align with the full model augmented by state fixed effects and potential covariates, even retaining statistical significance despite only considering a fourth of the number of observations. By any standard, the first round of NSP funding did not raise home prices.
While this evidence drives a nail into the coffin of foreclosure relief programs directly supporting anti-relief candidates, it still leaves open questions about the validity of the labor risk–equity model of voting explored in Chapter 3. Continuing the approach laid out above yields answers to two questions. First, could relief programs directly aid the efforts of anti-relief candidates? Second, in more general terms, are the effects of housing price changes magnified by low levels of home equity or high levels of labor risk?
4.3.2 Voting Impacts of the NSP and Price Changes
The next table lists the results of the full-sample models with and without accounting for prices. If the NSP’s primary effect was lowering prices, then we should expect that tracts targeted by the first round of the Neighborhood Stabilization Program saw lower levels of Republican voting after taking into account other related factors except price changes. Then, in the model including the price data, there should be no significant impact of NSP funding, as the only targets of the program were home prices. For the labor risk–equity model, in all trials there should be positive correlations between price changes and Republican voting, with augmented values where price changes refract through economic anxiety, as measured by high foreclosure rates (i.e. low equity) or risky employment (a.k.a. high unemployment variance).
| Dependent variable: | ||
| Republican vote percentage | ||
| (4) | (5) | |
| NSP1 | -0.5520** | -0.2498 |
| 2010 forelcosure rate | 0.4773*** | 2.2186*** |
| Home price change ’07–’10 | 0.0706** | |
| Labor risk | 0.5452*** | -0.2124*** |
| Unemployment change ’05–’10 | -0.1521* | -0.3227*** |
| Median household income (000s) | 0.1964*** | 0.1843*** |
| Population density | 0.0002*** | 0.0002*** |
| Tenure in home | -1.8314*** | -1.6090*** |
| Squared tenure | 0.0465*** | 0.0407*** |
| 65-and-up % | 0.1343*** | 0.0999*** |
| Black % | -0.0995* | -0.0505 |
| Hispanic % | 0.4195*** | 0.4169*** |
| Hispanic % squared | -0.0038*** | -0.0035*** |
| Asian % | 0.0564 | 0.1258** |
| White % | 0.2280*** | 0.2837*** |
| White: some college or less % | 0.1436*** | 0.1343*** |
| Evangelical % | 0.5286*** | 0.5403*** |
| L.D.S. % | 0.2319*** | 0.2839*** |
| Cook PVI 2008 | 0.6824*** | 0.7049*** |
| Price change foreclosure rate | 0.1345*** | |
| Price change labor risk | -0.0759*** | |
| Foreclosure rate density | -0.0001*** | -0.0001*** |
| White % some college or less | 0.0013*** | 0.0012*** |
| Constant | 6.0127 | 1.4107 |
| Observations | 27,098 | 27,098 |
| R2 | 0.4514 | 0.4654 |
| Adjusted R2 | 0.4510 | 0.4649 |
| Residual Std. Error | 14.9193 | 14.7292 |
| F Statistic | 1,114.1080*** | 1,024.6710*** |
| Note: | p<0.1; p<0.05; p<0.01 | |
Consistent with expectations, the presence of the Neighborhood Stabilization Program is associated with a half point lower Republican voting in the model without prices and significant at the 5% level. When taking into account prices, the presence of the Neighborhood Stabilization Program is not statistically significant, though still points negative. While there are reasons not to accept this model’s validity, the consistency of the expectations with the model—and prior literature—is a reason to believe its capacity to describe impacts of economic and demographic variables on majoritarian voting behavior. Down the line, from residential tenure through religious adherents, factors identified by prior research as impacting Republican turnout were similarly associated in my model.
Moreover, key features of the labor risk–equity model of political behavior found strong evidence in Model 5. The interaction effects between price changes, foreclosure rates, and labor risk are of interest here (uninteracted forms are provided for completeness and their effects are not predicted by the labor risk–equity literature). The magnifying effects of foreclosure rate on price changes was directly proportional, and price changes themselves were associated with more Republican voting. For instance, in our Palm Beach County tract 12099005947, my model estimated a 5.7-point increase in Republican vote share due to the combination of home price decline, foreclosure rate, and variance of employment. The interaction between prices and low equity (represented by foreclosures) holds a positive coefficient, consistent with the model’s prediction that low-equity and high-labor risk combine to decrease preferences for social insurance, tied in the United States to higher taxation.
The pairwise interaction between price change and labor risk carries an negative relationship with Republican voting. While an inverse relationship between labor risk and Republican voting should be expected, a negative relationship in the interaction term means that, controlling for other variables, an increase in labor risk means that risky employment actually causes more to vote Democratic (or, technically, non-Republican) as home prices increase. Or, to take the inverse of this statement, at low home prices (near foreclosure, for instance), people with risky employment savor their wealth and vote more Republican.
But the effects on the upper end pose some threat to the literature. This result was robust to the addition and subtraction of several covariates and subsets of the observations (results not shown). I account for it with post-crisis literature which argues that individuals with risky occupations face additional barriers to securing home equity lines of credit (HELOCs).176 Nuno Mota, “Spatial Features of Labor Markets and Links to the Housing Market” (https://www.semanticscholar.org/paper/Spatial-features-of-labor-markets-and-links-to-the-Mota/4092fc8ebb493a0b116f20a304bc7c9e4912f9d6, 2015), Table 1. Thus, rather than this negative association representing an inconsistency between predicted and actual effects of increased equity, it could be the case that incomplete credit markets prevented individuals with highly-risky employment from behaving as they would prefer. In sum, the labor risk–equity model and prior literature on Republican voting behavior broadly agree with my regression results on the full sample of observations.
Because of these reasons, I urge acceptance of the model’s capacity to understand the effects of certain economic variables on partisan voting behavior. Here it is important to understand this specific sense of model validity. The point here is not to predict vote outcomes, but to infer the effects of certain variables. While prediction would be nice (and would be sufficient to validate a model’s inferential power), all that need be true is that the unexplained variance be independent of the parameter(s) of interest. For instance, there is evidence that subprime mortgage brokers lent to Black and Latin-American families at systematically higher rates than White families;177 Gary Dymski, Jesus Hernandez, and Lisa Mohanty, “Race, Gender, Power, and the US Subprime Mortgage and Foreclosure Crisis: A Meso Analysis,” Feminist Economics 19, no. 3 (July 2013): 124–51, https://doi.org/10.1080/13545701.2013.791401; Faber, “Racial Dynamics of Subprime Mortgage Lending at the Peak.” since race is also associated with Republican voting, I have included the relevant descriptive variables in my models. Though I am worried about data quality with regards to ecological methods, the care taken to remove unobserved variable bias and the congruence of my results with expectations leads me to confidence in my model, and explains why I do not worry about fact that only half of the variation in Republican voting share is explained by my model.
How then did this model fare in Tea Party tracts? In these next trials, more pronounced home price effects should be expected, though it may also be possible that “deadbeat” homeowners are further stigmatized by Tea Party candidates, leading to more conservatizing effects of increased foreclosure rates. The following shows the results of the same model above, but applied only to tracts in which a self-described member of the Tea Party ran for election.
| Dependent variable: | ||
| Republican vote percentage | ||
| (6) | (7) | |
| NSP1 | -0.1615 | 0.1172 |
| 2010 forelcosure rate | -0.0137 | 0.7968*** |
| Home price change ’07–’10 | 0.2221*** | |
| Labor risk | 0.0843 | -0.6156*** |
| Unemployment change ’05–’10 | 0.3512*** | 0.3383*** |
| Median household income (000s) | 0.1745*** | 0.1807*** |
| Population density | -0.0002*** | -0.0002*** |
| Tenure in home | -1.5650*** | -1.4495*** |
| Squared tenure | 0.0379*** | 0.0344*** |
| 65-and-up % | 0.0979*** | 0.1019*** |
| Black % | -0.2138*** | -0.2353*** |
| Hispanic % | 0.1153** | 0.0861 |
| Hispanic % squared | -0.0010*** | -0.0011*** |
| Asian % | 0.1057* | 0.0889 |
| White % | 0.1872*** | 0.1546*** |
| White: some college or less % | 0.2016*** | 0.1977*** |
| Evangelical % | 0.3452*** | 0.3725*** |
| L.D.S. % | 0.3273*** | 0.3742*** |
| Cook PVI 2008 | 0.6658*** | 0.6852*** |
| Price change foreclosure rate | 0.0648*** | |
| Price change labor risk | -0.0608*** | |
| Foreclosure rate density | -0.0001*** | -0.0001*** |
| White % some college or less | 0.0010*** | 0.0012*** |
| Constant | 9.5495* | 12.1699** |
| Observations | 8,700 | 8,700 |
| R2 | 0.5729 | 0.5834 |
| Adjusted R2 | 0.5719 | 0.5823 |
| Residual Std. Error | 10.9460 | 10.8126 |
| F Statistic | 582.0408*** | 528.1887*** |
| Note: | p<0.1; p<0.05; p<0.01 | |
These trials offer promising results but less statistical significance.178 The [unprinted] p-value attached to Model 6 is just north of .10, nearly acceptable among social scientists. First, the evidence that NSP1 had any effect on voting is far from conclusive, with statistically insignificant associations between round one funding and Republican vote shares. Second, home price interaction terms are significant and carry the same signs as in trials run on the full slate of observations, but insignificant when uninteracted. Third, the foreclosure rate switches signs when combined with the effects of home prices. This switch means that apart from their effects on prices foreclosures are associated with increased Republican voting, but when those [negative] price effects are included, voters choose Democratic candidates more. This finding agrees with the narrative that Tea Party candidates cast foreclosed homeowners as irresponsible and blame-worthy neighbors, though my principal question about differential effects of price changes did not yield conclusive results.
It seems that, since the NSP is associated with higher rates of Republican voting in the face of negative price effects, cultural (rather than economic) factors may have been at play. One explanatory theory is the patronage model of voting, otherwise known as you scratch our back, and we’ll scratch yours. A comparison of how each of the NSP rounds fared with respect to Republican votes is available in the following table. The first round saw statistically-insignificant effects on Republican voting, while rounds two and three saw decreases in Republican vote share of 3.1% and 5.7% respectively. I excluded the second and third NSP rounds in my formal analysis because, as of July 2011, respectively 20.6% and 0.4% of funds had been expended from NSP2 and NSP3.179 18568, “HUD NSP3 Report: National Expenditures by Grantee (Q2 2011)” (Department of Housing and Urban Development, July 2011); 18568, “HUD NSP2 Report: National Expenditures by Grantee (Q2 2011)” (Department of Housing and Urban Development, July 2011). Though NSP1 had expended 43.4% of funds and fully committed its allocations to grantees by September 2010,180 18568, “HUD NSP-1 Reporting Sept 2010: Program-Wide Detail Report” (Department of Housing and Urban Development, November 2010). the analysis of housing prices above demonstrates that the program had not yet (if it had eventually) raised prices for recipients. This fact implies that even later rounds had less time to deploy price-stabilization measures. Thus, any perceived effects could not been due to the price effects sought by the program, but rather by those factors which caused HUD to designate such tracts for funding, and I propose, by the designation itself. By directing funding towards these neighborhoods, administrations could try to implement a licit form of vote buying. That these effects would be so pronounced, and that residents would not also be motivated by an anti-welfare pride, is difficult to believe, however.
| Dependent variable: | |||
| Republican vote percentage | |||
| (4) | (10) | (11) | |
| NSP1 | -0.2498 | ||
| NSP2 | -3.0834*** | ||
| NSP3 | -5.7479*** | ||
| 2010 forelcosure rate | 2.2186*** | 2.2286*** | 2.2544*** |
| Home price change ’07–’10 | 0.0706** | 0.0629** | 0.0704** |
| Labor risk | -0.2124*** | -0.2105*** | -0.2054*** |
| Unemployment change ’05–’10 | -0.3227*** | -0.2933*** | -0.3265*** |
| Median household income (000s) | 0.1843*** | 0.1834*** | 0.1814*** |
| Population density | 0.0002*** | 0.0002*** | 0.0002*** |
| Tenure in home | -1.6090*** | -1.5979*** | -1.5884*** |
| Squared tenure | 0.0407*** | 0.0403*** | 0.0402*** |
| 65-and-up % | 0.0999*** | 0.0975*** | 0.1008*** |
| Black % | -0.0505 | -0.0579 | -0.0563 |
| Hispanic % | 0.4169*** | 0.4077*** | 0.4101*** |
| Hispanic % squared | -0.0035*** | -0.0035*** | -0.0035*** |
| Asian % | 0.1258** | 0.1200** | 0.1165** |
| White % | 0.2837*** | 0.2754*** | 0.2797*** |
| White: some college or less % | 0.1343*** | 0.1339*** | 0.1380*** |
| Evangelical % | 0.5403*** | 0.5323*** | 0.5354*** |
| L.D.S. % | 0.2839*** | 0.2796*** | 0.2947*** |
| Cook PVI 2008 | 0.7049*** | 0.7151*** | 0.7065*** |
| Price change foreclosure rate | 0.1345*** | 0.1359*** | 0.1313*** |
| Price change labor risk | -0.0759*** | -0.0753*** | -0.0743*** |
| Foreclosure rate density | -0.0001*** | -0.0001*** | -0.0001*** |
| White % some college or less | 0.0012*** | 0.0013*** | 0.0012*** |
| Constant | 1.4107 | 2.1849 | 1.9728 |
| Observations | 27,098 | 27,098 | 27,098 |
| R2 | 0.4654 | 0.4664 | 0.4670 |
| Adjusted R2 | 0.4649 | 0.4659 | 0.4666 |
| Residual Std. Error | 14.7292 | 14.7156 | 14.7061 |
| F Statistic | 1,024.6710*** | 1,028.7220*** | 1,031.5750*** |
| Note: | p<0.1; p<0.05; p<0.01 | ||
Explaining the cultural dynamics of this phenomenon (and teasing out its existence) opens opportunities for further research, but I present one theory now. Eagle-eyed readers will have noted that, while the foreclosure rate and population density were included in Section 3.3, the interaction between them was left unexplained. I have included this term to measure sociological effects of foreclosures, namely social contact theory, which posits that contact with an Other causes members of the in-group to sympathize with said Other. In this case, that Other is foreclosed homeowners. Where density is low, it may be possible to avoid seeing or knowing one of these “deadbeats”, but as densities (and foreclosure rates) rise, it becomes less and less possible to assimilate ideas of irresponsibility and blame with people that one knows personally. While the coefficient attached to the foreclosure rate–population density interaction term is small, it was statistically significant in every trial I ran. Further, population density carries an enormous range of values; while most of these predictors are bounded between 0 and 100 percent, population density ranges from 0 to nearly 80,000. As such, the interaction term ranges from 0 to 270,896.7, meaning that effects could be quite large at the upper end.
4.3.3 Limitations and proposed refinements
However, even with all these statistically-significant terms, there are questions of model adequacy that I am poorly-equipped to address. These models were limited by several factors, but the three areas I focus on as most important are data quality, model fitness, and spatial dependence. My data quality concerns are ever-present in natural-experiment methodologies. In short, individual voting characteristics, more granular price data, and a fuller spread of census tracts could have aided the conclusivity of this evidence. Additionally, using individual-level demographics and vote results would have avoided the ecological assumptions this analysis rests on.
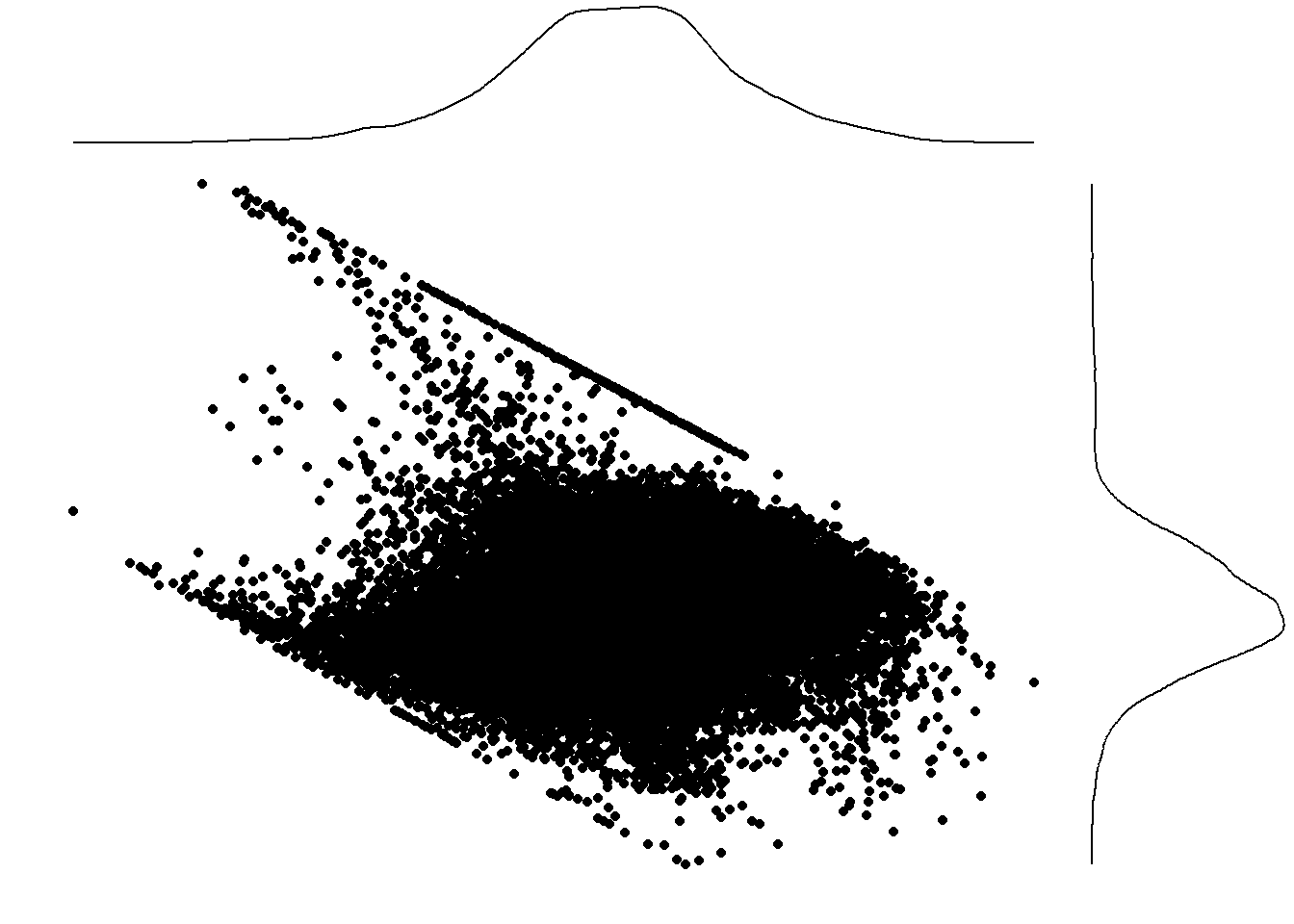
 Figure 4.7: Diagnostic plots of the full linear model.
Figure 4.7: Diagnostic plots of the full linear model.
The second question, of model fitness, leaves for more ambiguous refinements. In inferential statistics, there is less of a need for a model to fit the data comprehensively. On that count, the attached .45-.58 \(R^{2}\) values are not concerning. However, further analysis of the residuals demonstrates weaknesses in model selection. Figure 4.7 shows the residuals against fitted values for the full-sample, fixed-effects model, as well as the quantile-quantile distribution of residuals. Ideally, residuals show no conclusive pattern, and are independent against the fitted values. Here, there is a clear inverse relationship framed by the bounds of the Republican voting share at 0 and 100 percent. Linear models are not built to handle bounded response variables, though I used one for the ease of computation and interpretation.
In order to validate the results of these models, I also modeled Republican vote share by different distributions. I settled on reporting results for regressions on the Beta distribution because of its flexibility181 Francisco Cribari-Neto and Achim Zeileis, “Beta Regression in R,” Journal of Statistical Software 34, no. 1 (April 2010): 1–24, https://doi.org/10.18637/jss.v034.i02. and ability to approximate the distribution of Republican voting share. The Beta distribution is a fundamental (but complicated) distribution used for response variables bounded between 0 and 1. It easily incorporates changing variance and does not assume linearity, which is helpful when considering social interactions generally, and electoral data specifically.
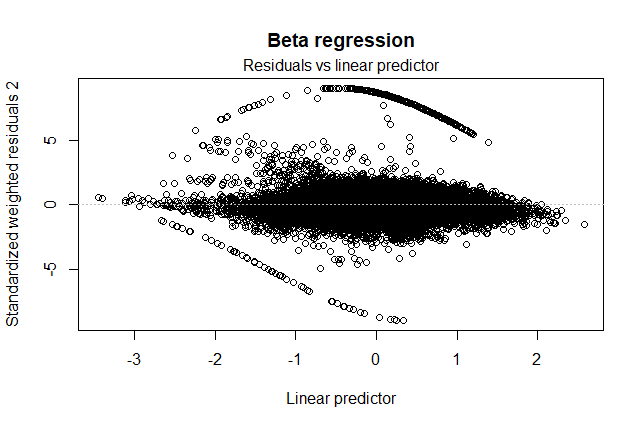 Figure 4.8: Standardized weighted residuals of full beta regression.
Figure 4.8: Standardized weighted residuals of full beta regression.
Though there are still the artifacts of upper and lower bounds, the behavior of Figure 4.8 conforms more closely to an ideal distribution. Results of the beta regressions can be seen in the next table. Coefficients are altogether similar182 For entirely computational reasons, the dependent variable, Republican voting percentage, had to be scaled to fit between 0 and 1. The predictors, therefore, were also reduced by a factor of 100 in order to remain comparable to the linear models. While this adjustment worked on all independent variables, the interaction terms—which had been products of numbers between 0 and 100—were then made to be products of numbers between 0 and 1. This translation is analogous to that from 10 to 0.1: \(10 \times 10 = 100\), growing in magnitude, while \(.1 \times .1 = .01\), shrinking by the same number of decimal places. to what the linear models predict, making me more secure in my belief of their validity.
| Dependent variable: | ||
| Republican vote percentage | ||
| (8) | (9) | |
| NSP1 | -0.0346*** | -0.0255** |
| 2010 forelcosure rate | 3.6235*** | 12.4097*** |
| Home price change ’07–’10 | -0.0809 | |
| Labor risk | 2.9805*** | -0.9525*** |
| Unemployment change ’05–’10 | -2.3280*** | -3.5841*** |
| Median household income (000s) | 0.7244*** | 0.6358*** |
| Population density | 0.0015*** | 0.0019*** |
| Tenure in home | -6.7616*** | -5.8044*** |
| Squared tenure | 0.1583*** | 0.1373*** |
| 65-and-up % | 0.4107*** | 0.2241*** |
| Black % | -1.4347*** | -0.9964*** |
| Hispanic % | 1.6276*** | 1.6829*** |
| Hispanic % squared | -0.0210*** | -0.0191*** |
| Asian % | -0.4704* | |
| White % | 0.6734** | 1.0943*** |
| White: some college or less % | 0.9696*** | 0.8997*** |
| Evangelical % | 2.5835*** | 2.6260*** |
| L.D.S. % | 0.5231 | 0.5277 |
| Cook PVI 2008 | 0.0172*** | 0.0195*** |
| Price change foreclosure rate | 73.2971*** | |
| Price change labor risk | -39.4921*** | |
| Foreclosure rate density | -0.0806*** | -0.0738*** |
| White % some college or less | 0.0125 | -0.0356 |
| Constant | -1.4635*** | -1.7904*** |
| Observations | 27,098 | 27,098 |
| R2 | 0.2940 | 0.3119 |
| Log Likelihood | 9,807.5620 | 10,187.4100 |
| Note: | p<0.1; p<0.05; p<0.01 | |
Lastly, as mentioned, these models were spatially-dependent, which biased the estimation of the home price effect on voting behavior. Using state-level fixed effects and tract-level housing prices corrected some of this behavior, but the local nature of politics cannot be underestimated. I had originally planned to incorporate spatial autoregressive methods to correct for this spatial dependence, but limitations inherent to my data, as well as a lack of remote access to better hardware, quashed that opportunity.183 This chapter was completed during 2020’s novel coronavirus pandemic, which restricted access to University resources. Nonetheless, I can prove the presence of spatial dependence in my models to highlight future areas for exploration.184 Roger S. Bivand and David W. S. Wong, “Comparing Implementations of Global and Local Indicators of Spatial Association,” TEST 27, no. 3 (September 2018): 716–48, https://doi.org/10.1007/s11749-018-0599-x.
I first constructed a matrix of neighboring census tracts using geographic tract files; this matrix tells R which tracts are neighbors by triangulating their population-weighted geographic centers. I then ran the residuals of each model (from a positivist interpretation, these are the unobserved variables) through Moran’s I and Geary’s C tests. The similar tests look for spatial dependence respectively at the global and local levels. Since this dataset is fractured, containing large discontiguities, Geary’s C test will be the more appropriate measure; both are retained because the calculations are quick and similar. Table 4.1 displays the results of these tests, all of which reject the null hypothesis of no spatial dependence, affirming Tobler’s first law of geography that “everything is related to everything else, but near things are more related than distant things.”185 Tobler, “A Computer Movie Simulating Urban Growth in the Detroit Region,” 236.
Table 4.1: Results of various tests for spatial dependence. In all tests, the null hypothesis is spatial independence.
| Model | Moran’s I | Moran p-value | Geary’s C | Geary p-value |
|---|---|---|---|---|
| Full-sample no prices | 0.7738 | 0 | 0.2369 | 0 |
| Full-sample with prices | 0.7674 | 0 | 0.2436 | 0 |
| Tea Party no prices | 0.6984 | 0 | 0.3180 | 0 |
| Tea Party with prices | 0.6872 | 0 | 0.3298 | 0 |
| Beta full sample | 0.7641 | 0 | 0.2469 | 0 |
| Beta just Tea Party | 0.6420 | 0 | 0.3748 | 0 |
4.4 Conclusion
In sum, 2010 prices were negatively associated with the Neighborhood Stabilization Program’s first round of funding. Perhaps this result was due to unobserved variable bias, but, given the normalcy of regression diagnostics, and the results of later NSP rounds, it may instead result from the NSP’s timeline. Due to the legislative mandate that grantees purchase homes at a slight discount, there may not have been enough time to clear, repair, and re-appraise (or fully resell) properties by the 2010 midterms. My results indicate that the NSP reduced prices between 1.4% and 2.0%, a small reduction keeping with size of the mandated discount. Further, by NSP1’s maturation in 2013, the amount of funds spent on acquisitions dropped, while new construction and rehabilitation increased slightly compared to its 2010 progress.186 18568, “HUD NSP-1 Reporting: Sept 2010 Program-Wide Report” (Department of Housing and Urban Development, November 2010); HUD, “HUD NSP1 Report: National Drawdowns by Activity (Q3 2013)” (Department of Housing and Urban Development, n.d.).
The labor risk–equity model was evaluated in spite of this fact, and evidence suggested the theorized effects were present in the 2010 midterms, though oddly not when only Tea Party tracts were considered. Economic anxiety, composed of low equity and risky employment magnified the conservatizing effects of increased home prices. These results were statistically significant and robust to several covariates. Still to be explained are the mechanisms by which labor risk propagates through mortgage markets, HELOCs, and political behavior. This variable proved “liberalizing”, in tension with prior literature on the subject.
Limitations of the measurement and statistical methods were explored, with strong evidence that further work is needed to extricate the impacts studied from spatial dependence and bounded response assumptions. Beta distribution regression was employed to correct for the latter issue, with slightly more ideal measures of model fitness and similarly strong evidence for the labor risk–equity model’s capacity to explain voter behavior in the full sample as well as the Tea Party tracts. These results build towards consensus with empirical literature, girding Ansell (2014) with voting results to provide a crucial middle step in his argument.